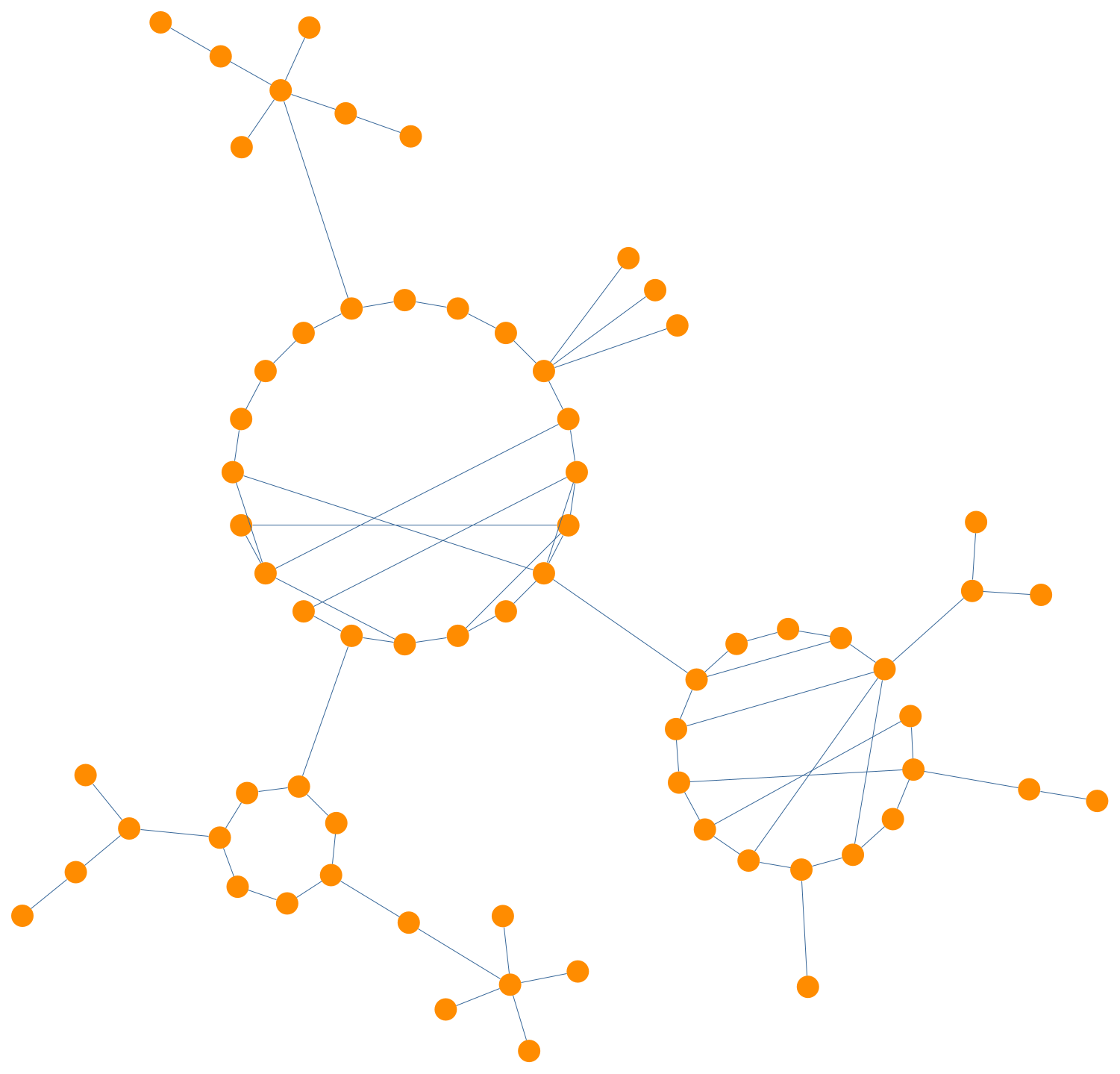
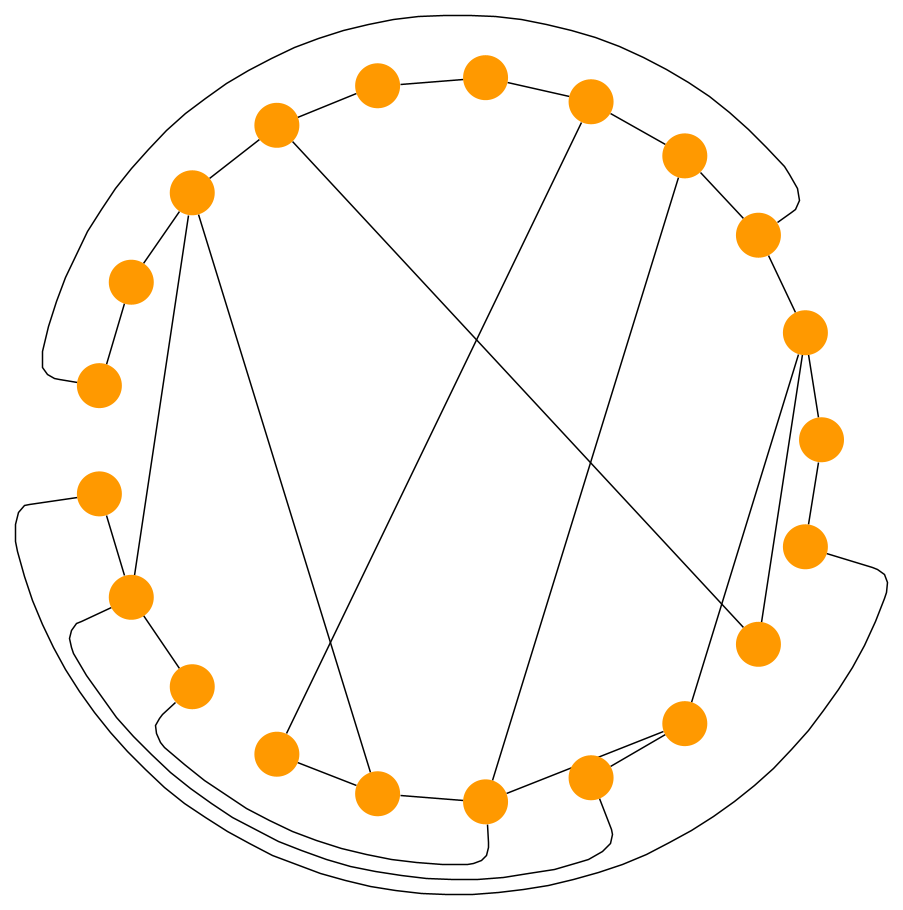
Circular Graph Layout
The different options of arranging diagram elements in circles
A circular layout graph drawing algorithm places the nodes of a graph on circles, as shown below. The resulting diagrams often expose connected components and their inter-dependencies along with potential tree structures of the graph.
Circular layouts find applications in many fields such as social networking, network management, WWW visualization, eCommerce, telecommunications, and they can be quite efficient for large graphs.
How does Circular Layout work?
-
The algorithm partitions the nodes of the graph based on specific criteria, e.g., connectivity and by taking into account the desired layout style, e.g., single or multiple circles.
-
Each such partition constitutes a single node that only has edges to other related partitions. Thus, the resulting graph obtains a tree-like structure (the so-called underlying tree).
-
The algorithm arranges each partition as a circle. Depending on the desired style, each circle has nodes either on the boundary or in the interior.
-
A specialized approach for tree structures calculates the arrangement of the underlying tree.
-
The algorithm moves the partitions to their final location.
Circular Layout of yFiles
Automatic layout algorithms are one of the critical features of the commercial programming library yFiles. yFiles provides a very sophisticated implementation of the circular graph layout algorithm that is well suited for both small and large graphs and can easily be configured.
Furthermore, it supports the following advanced features.
Layout Style Options
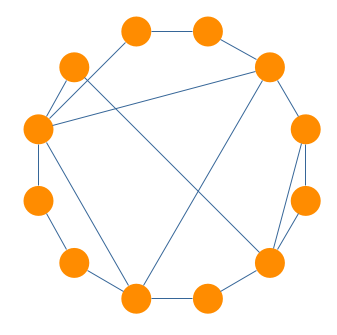
The layout style determines which policy the algorithm should follow to partition the nodes of the graph. More precisely, each partition can represent a so-called biconnected component of the graph. A biconnected component consists of nodes that are reachable by two edge-disjoint paths. In this case, nodes belonging to more than one biconnected component are assigned exclusively to one partition (see BCC-Compact Layout StyleBCC-Compact Layout Style) or to a separate partition (see BCC-Isolated Layout StyleBCC-Isolated Layout Style). It is also possible to place all nodes on a single circle (see Single Cycle Layout StyleSingle Cycle Layout Style) or on multiple circles defined by the user (see Custom Groups Layout StyleCustom Groups Layout Style).
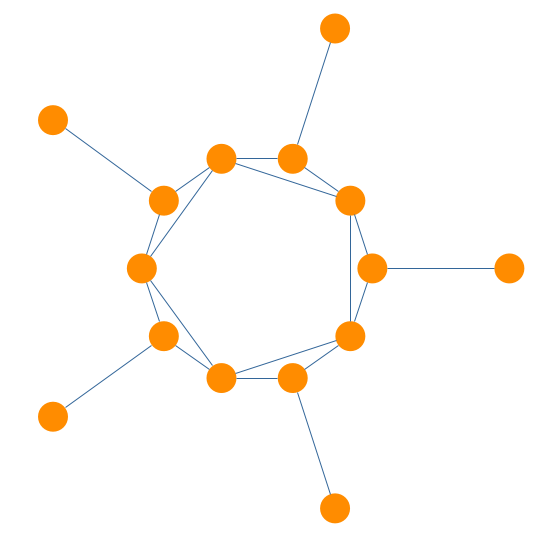
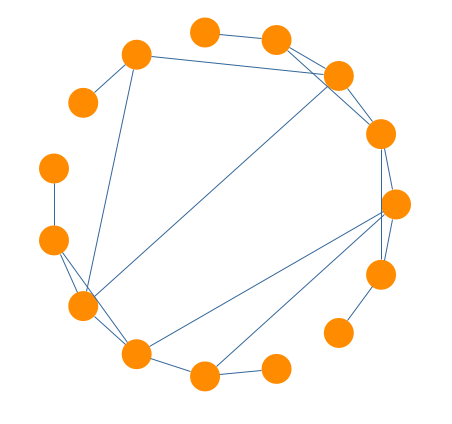
Partition Arrangement Options
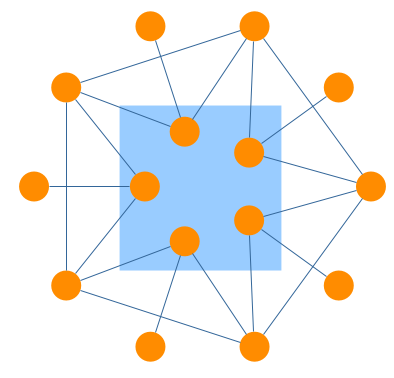
The user can also specify how the algorithm arranges the nodes within a partition. More precisely, the nodes can be placed on the boundary of a given partition (see Partition Style CirclePartition Style Circle) or on a disk. In a disk arrangement, nodes of a given partition connected to nodes of other partitions are placed on the disk’s boundary while all other nodes in the interior (see Partition Style DiskPartition Style Disk) of the disk. Similar is the organic disk, which uses an organic approach to arrange the nodes of a partition. Nodes that connect to nodes of other partitions can be placed both in the interior or on the boundary of the disk (see Partition Style Organic DiskPartition Style Organic Disk).
Edge Bundling
Edge bundling refers to bundling together multiple edges so that their common parts are, to some degree, merged into a bundled part. It is useful for increasing the readability of graph drawings with a high number of edges which suffer in most cases of visual cluttering and bad feature readability. The circular layout algorithm also supports this feature and bundles edges at their common parts. At the source and target points, the edges are again clearly split.
Exterior Edge Routing
Exterior Edge Routing refers to routing (a subset of) edges that belong to the same partition around the exterior of the associated circle. This can significantly improve the readability of the layout by reducing the edge clutter in the interior of the circles. Therefore, this is a suitable option mainly when having partitions or single cycles where the nodes are highly connected with each other. The following example was calculated with the circular layout algorithm of yFiles.